10 Laplace Transform and Transfer Function
The previous chapters have focused on understanding the dynamics of the system by observing the output of the system for specified inputs. For example, when a constant rudder and propeller rate are provided as inputs, the vessel executes the turning circle maneuver. The characteristics of the response were quantified through metrics such as advance, transfer, tactical diameter, steady turning radius etc. This and the following chapters will focus on trying to control the response of the system (motion of the vessel) to exhibit a desired behavior.
Chapter 1, Chapter 2 and Chapter 3 saw the derivation of kinematic and dynamic equations of motion of a marine craft. These differential equations govern the motion of the vessel for a general control input provided to the vessel. Thus, the differential equations can be represented as a system as shown in Figure 10.1 that takes propeller rate and rudder angle as inputs and outputs the motion of the vehicle. The representation shown in Figure 10.1 is known as block diagram representation. System is also sometimes referred to as plant in control terminology.

There are two main objectives of a control system:
The first objective is to determine the input to be provided to the system so that the output tracks or follows a desired output. This phenomenon of output following a desired output is known as tracking.
The second objective is to ensure that the output tracks the desired output even in the presence of disturbances. This phenomenon is known as disturbance rejection.
10.1 Open and Closed Loop Control
Open loop control refers to the case where the control input is independent of the system output. This is also known as feed forward control. Based on the desired output, the controller calculates the required input to the system that allows the system response to track the desired output. In the open loop control strategy, the controller must have inverse dynamics of the system. The block diagram for open loop controller is shown in Figure 10.2.

Consider a room with an air conditioner where running the air conditioner for one hour results in the room temperature to reduce to \(20^{\circ}\) from an ambient temperature of \(25^{\circ}\). Running the air conditioner every night for one hour to achieve a room temperature of \(20^{\circ}\) is an example of open loop control. Notice that the control input of how long to run the air conditioner does not depend upon the room temperature. Thus when the ambient temperature is \(30^{\circ}\), the open loop control will not be able to track the desired response of \(20^{\circ}\) room temperature. Thus open loop control cannot correct for any disturbances (ambient temperature not being \(25^{\circ}\)). Similarly, the same open loop control when applied to a room of different size will not yield the same response. Thus, the open loop control cannot account for errors in modelling of the plant.
These limitations can be overcome by the introduction of feedback. Feedback controller or a closed loop controller takes as input the error between the desired output and the current output of the plant to provide the required control input to the plant. The block diagram for the feedback control is shown in Figure 10.3.
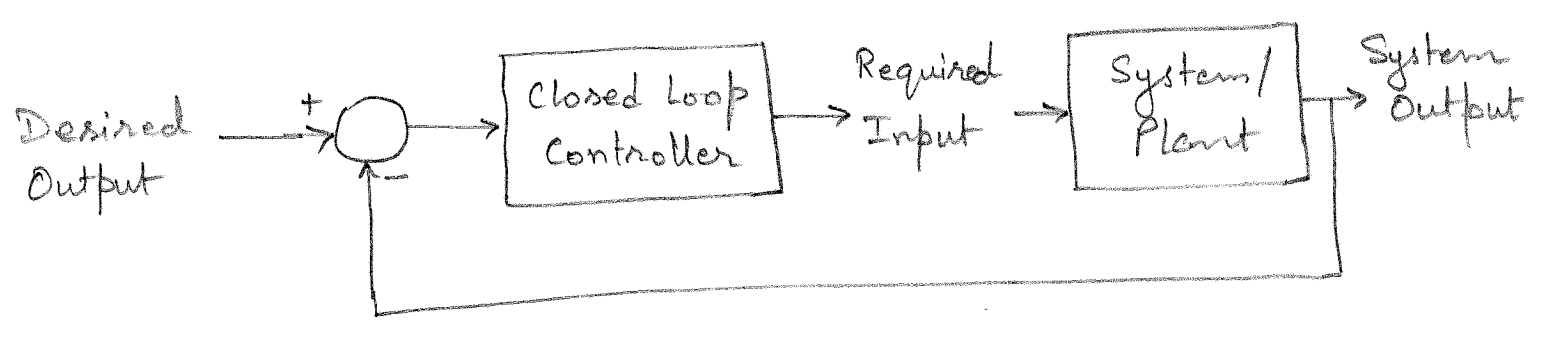
Feedback control or closed loop control strategies can overcome the limitations of the open loop control. Once tuned, the feedback controllers can perform both tracking as well as disturbance rejection well even when the plant model is not accurately known. It will be later shown that some mathematical guarantees can be provided on their performance.
10.2 Laplace Transform
A simple example of a control problem for a marine vehicle is to maintain a particular heading at sea. Assuming that the yaw dynamics for the vessel is governed by Nomoto’s first order model
\[\begin{align} T\dot{r} + r = K\delta \end{align}\]
the stability of the system can be determined by assuming a steady state input \(\delta = \delta_0 e^{st}\) and a steady state output \(\psi = \psi_0 e^{st}\). Substituting the steady state input and output into the Nomoto model yields
\[\begin{align} (Ts^2 + s) \psi_0 e^{st} = K \delta_0 e^{st} \end{align}\]
The ratio of amplitudes of output to input is known as the transfer function for the system and is a function of \(s\) as shown below.
\[\begin{align} \frac{\psi_0}{\delta_0} = G(s) = \frac{K}{s(Ts + 1)} \label{eq-transfer-function-1} \end{align}\]
This transformation of a linear system from time domain (involving differential equations) to the \(s\)-domain (involving algebraic equations) is known as Laplace transform. Formally, the Laplace transform of any function \(f(t)\) is given by
\[\begin{align} \mathcal{L} \left\{f(t)\right\} = F(s) = \int_0^{\infty} f(t) e^{-st} dt \label{eq-laplace-transform} \end{align}\]
Similar to the Laplace transform, the inverse Laplace transform of a function in \(s\)-domain is given by
\[\begin{align} f(t) = \mathcal{L}^{-1} \left\{ F(s) \right\} = \frac{1}{2\pi i} \lim_{\omega \rightarrow \infty} \oint_{\sigma - i \omega}^{\sigma + i \omega} F(s) e^{st} ds \label{eq-inv-laplace-transform} \end{align}\]
where \(\sigma\) is chosen such that the contour path of integration is in the region of convergence of \(F(s)\).
The integral definitions shown in \(\eqref{eq-laplace-transform}\) and \(\eqref{eq-inv-laplace-transform}\) are not evaluated practically. Rather the properties of Laplace transforms are used to simplify the transfer functions into simplified units whose inverse transform is known. Some of the common Laplace and inverse Laplace transform pairs are listed in Table 10.1. This table is not exhaustive, but contains the commonly used Laplace transforms.
| Sl. no. | \(f(t) = \mathcal{L}^{-1} \left\{F(s)\right\}\) | \(F(s) = \mathcal{L} \left\{f(t)\right\}\) |
|---|---|---|
| \(1\) | \(1\) | \(\frac{1}{s}\) |
| \(2\) | \(e^{at}\) | \(\frac{1}{s-a}\) |
| \(3\) | \(t^n\) for \(n=1,2,3,...\) | \(\frac{n!}{s^{n+1}}\) |
| \(4\) | \(t^p\) for \(p>-1\) | \(\frac{\Gamma(p+1)}{s^{p+1}}\) |
| \(5\) | \(\sqrt{t}\) | \(\frac{\sqrt{\pi}}{2s^{3/2}}\) |
| \(6\) | \(t^{n - \frac{1}{2}}\) for \(n=1,2,3,...\) | \(\frac{1.3.5...(2n-1)\sqrt{\pi}}{2^n s^{n+\frac{1}{2}}}\) |
| \(7\) | \(\sin(at)\) | \(\frac{a}{s^2 + a^2}\) |
| \(8\) | \(\cos(at)\) | \(\frac{s}{s^2 + a^2}\) |
| \(9\) | \(t\sin(at)\) | \(\frac{2as}{\left(s^2 + a^2\right)^2}\) |
| \(10\) | \(t\cos(at)\) | \(\frac{s^2 - a^2}{\left(s^2 + a^2\right)^2}\) |
| \(11\) | \(\sin(at + b)\) | \(\frac{s \sin(b) + a\cos(b)}{s^2 + a^2}\) |
| \(12\) | \(\cos(at + b)\) | \(\frac{s \cos(b) - a\sin(b)}{s^2 + a^2}\) |
| \(13\) | \(\sinh(at)\) | \(\frac{a}{s^2 - a^2}\) |
| \(14\) | \(\cosh(at)\) | \(\frac{s}{s^2 - a^2}\) |
| \(15\) | \(e^{at}\sin(bt)\) | \(\frac{b}{(s-a)^2 + b^2}\) |
| \(16\) | \(e^{at}\cos(bt)\) | \(\frac{s-a}{(s-a)^2 + b^2}\) |
| \(17\) | \(e^{at}\sinh(bt)\) | \(\frac{b}{(s-a)^2 - b^2}\) |
| \(18\) | \(e^{at}\cosh(bt)\) | \(\frac{s-a}{(s-a)^2 - b^2}\) |
| \(19\) | \(t^n e^{at}\) for \(n=1,2,3,...\) | \(\frac{n!}{(s-a)^{n+1}}\) |
| \(20\) | \(f(ct)\) | \(\frac{1}{c}F\left(\frac{s}{c}\right)\) |
| \(21\) | Heaviside function \(H(t-c) = \begin{cases} 1 \text{ for } t\geq c \\ 0 \text{ for } t<c\end{cases}\) | \(\frac{e^{-cs}}{s}\) |
| \(22\) | Dirac delta function \(\delta(t-c)\) | \(e^{-cs}\) |
| \(23\) | \(H(t-c)f(t-c)\) | \(e^{-cs}F(s)\) |
| \(24\) | \(\delta(t-c)g(t)\) | \(e^{-cs} \mathcal{L}\left\{g(t+c)\right\}\) |
| \(25\) | \(e^{ct}f(t)\) | \(F(s-c)\) |
| \(26\) | \(t^nf(t)\) for \(n=1,2,3,...\) | \((-1)^n \frac{d^nF}{ds^n}(s)\) |
| \(27\) | \(\frac{f(t)}{t}\) | \(\int_0^s F(u)du\) |
| \(28\) | \(\int_0^t f(v) dv\) | \(\frac{F(s)}{s}\) |
| \(29\) | \(\int_0^t f(t-\tau)g(\tau) d\tau\) | \(F(s)G(s)\) |
| \(30\) | \(f'(t)=\frac{df}{dt}\) | \(sF(s) - f(0)\) |
| \(31\) | \(f''(t)=\frac{d^2f}{dt^2}\) | \(s^2F(s) - sf(0) - f'(0)\) |
| \(32\) | \(f^{(n)}(t)=\frac{d^nf}{dt^n}\) | \(s^nF(s) - s^{n-1}f(0) ... -sf^{(n-2)}(0) - f^{(n-1)}(0)\) |
Going back to the problem of maintaining a heading for a marine vessel, the transfer function between heading \(\psi\) and rudder angle \(\delta\) is given by
\[\begin{align} G(s) = \frac{K}{s(Ts+1)} = \frac{K}{s} - \frac{K}{s + \frac{1}{T}} \label{eq-nomoto-heading-tf} \end{align}\]
Thus the response of the system to an impulsive rudder (applied only for an instant at \(t=0\)), obtained by taking an inverse Laplace transform of \(\eqref{eq-nomoto-heading-tf}\) and is shown below.
\[\begin{align} g(t) = \mathcal{L}^{-1}\left\{G(s)\right\} = K - Ke^{-\frac{t}{T}} \end{align}\]
It can be seen that for \(T>0\), the exponential part will decay to zero as \(t \rightarrow 0\). Thus for \(T>0\) the ship will settle onto a constant heading given by \(\psi = K\) if the initial heading was \(\psi(0)=0\). This means that the vessel is straight line stable. Although this is already known from the discussion in Chapter 5, the above analysis shows the previous analysis extended to the time domain using inverse Laplace transform.
From the previous discussion in Chapter 5, it is known that the coefficient of time in the exponential term of the response corresponds to the value of \(s\) at which the transfer function is infinite. These values are known as poles of the system. Formally, for a transfer function \(G(s) = \frac{N(s)}{D(s)}\) with polynomial numerator \(N(s)\) and polynomial denominator \(D(s)\)
\[\begin{align} \text{Poles} &= \left\{s | G(s)=\infty \text{ and } D(s)=0 \text{ such that } N(s)\neq 0\right\} \nonumber \\ \text{Zeros} &= \left\{s | G(s)=0 \text{ and } N(s)=0 \text{ such that } D(s)\neq 0\right\} \nonumber \end{align}\]
For a system response to be stable, the poles of the system must lie in the left half of the complex \(s\)-plane. For the Nomoto first order model, \(T>0\) implies that the pole of the system \(s=\frac{-1}{T}\) lies in the left half complex \(s\)-plane.
The next chapter will describe the performance metrics for a control system and focus on how these metrics correspond to the location of the poles of the transfer function in the complex \(s\)-plane.